Graphics, Figures & Tables ⇒ Quadratic fractal with TikZ

[Tobias_G]

Dear all,

I would like to create a fractal similar to the Koch snowflake using TikZ:

Code: Select all

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{lindenmayersystems}
\begin{document}
\begin{tikzpicture}
\draw [l-system={rule set={F -> F-F++F-F}, step=2pt, angle=60,
   axiom=F++F++F, order=4}] lindenmayer system -- cycle;
\end{tikzpicture}
\end{document}

What do I have to change in the code above so that the outcome looks like the attached graphic? (One starts with a square of sidelength 1, then one attaches in the middle of each side a new square with sidelength 1/3 and so on...)

Thanks for your help!

[Stefan Kottwitz]

Hi Tobias,

the fractal image is built of 4 identical parts, so generate the basic part and built it together by an axiom like F+F+F+F with an angle of 90 degrees.

In contrast to the Koch snowflake, not each line is recursively replaced. This can be solved using two different rules.

So here's an approach:

Code: Select all

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{lindenmayersystems}
\begin{document}
\begin{tikzpicture}
  \draw [l-system={rule set={G -> F-G+G+G-F, F -> FF}, step=2pt, angle=90,
         axiom=G+G+G+G, order=3}] lindenmayer system -- cycle;
\end{tikzpicture}
\end{document}

The versions up to level 4, scaling omitted:

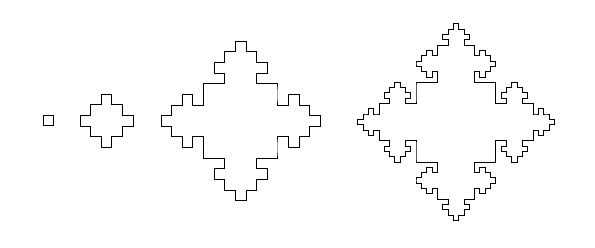
fractal.png (3.79 KiB) Viewed 5680 times

It still seems to need a bit of adjusting line lengths, to exact match the image.

Stefan

[Tobias_G]

Hi Stefan,

thank you very much for your quick an enlightening response!

How can I adjust the line lengths?

Tobias

[Stefan Kottwitz]

Another rule is useful here:

Code: Select all

\draw [l-system={rule set={G -> F-G+G+G-F, F -> FFH, H -> FF}, step=2pt, angle=90,
       axiom=G+G+G+G, order=3}] lindenmayer system -- cycle;

Tested with order 3 and 5 (used \begin{tikzpicture}[scale=0.40,transform shape] to scale it down then)

square-fractal.png (4.72 KiB) Viewed 5661 times

Stefan

[Tobias_G]

Stefan,

you are a LaTeX-BOSS !

Thank you so much for your help.
Tobias